FlashAttention
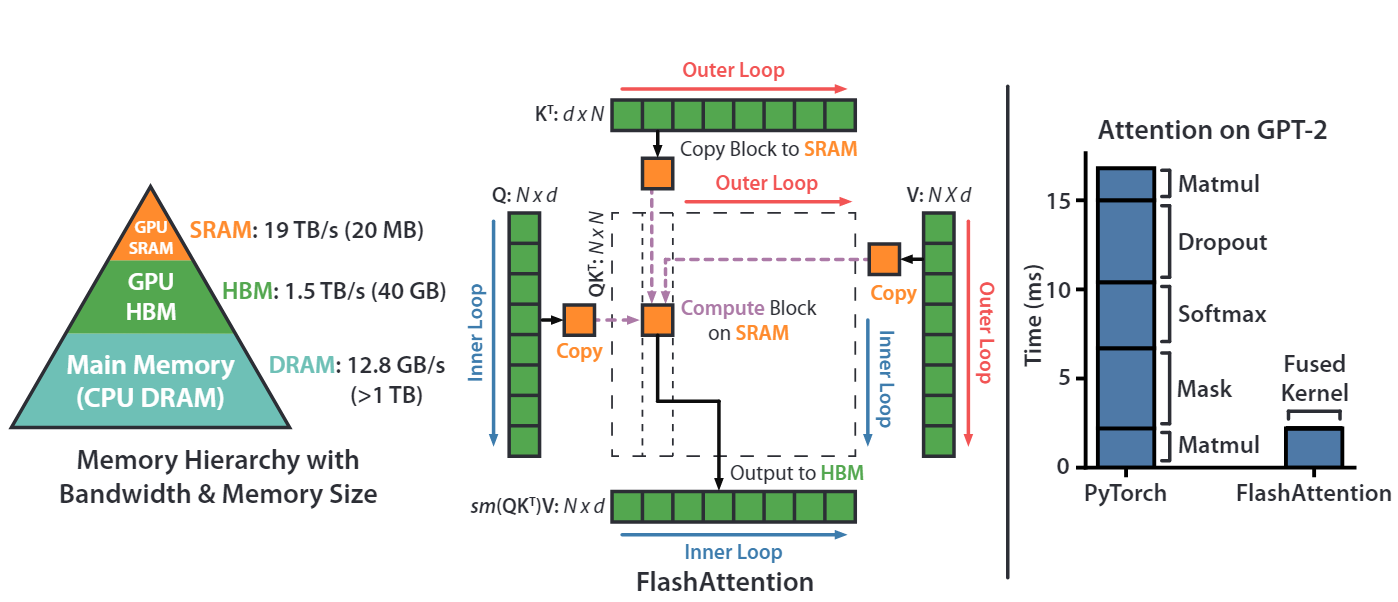
传统Attention实现

FlashAttention实现

FlashAttention 如何分块计算
FlashAttention 的目标是:不生成完整的 N×N 矩阵,同时计算结果完全一致。
在FlashAttention中,分块操作是针对序列长度(N)进行的,而不是直接将整个N×N矩阵切成小块。具体来说:
- 输入矩阵的维度:
- 假设输入序列长度 N=8000,每个词向量维度 d=64。
- 矩阵 Q 和 K 的维度均为8000×64,矩阵 V 也是 8000×64。
-
分块的目标:
- 将 Q 按行(序列维度)分成多个小块 Q1,Q2,…,Q80,每个块大小 100×64(共 8000/100=80块)。
- 同理,将 K 和 V 也按行分成 80 个块,每个块 100×64。
- 分块计算的逻辑:
- 不直接计算完整的 N×N矩阵,而是逐块计算Q_i × K_j ^ T(其中i,j 从1到80)。
-
每个 Q_i × K_j ^ T 的结果是一个 100×100 的注意力分数块S_ij (6400个100×100),属于最终 8000×8000 矩阵的一部分。
-
对S_ij做局部Softmax,得到注意力权重块 P_ij (P=softmax(S))。
-
计算 P_ij × V_j → 得到 100×64 的局部输出块,将该局部输出块累加到 O(初始化输出矩阵,8000×64) 的第 i行块中。
FlashAttention 的分块 Softmax 实现
Softmax演进
Naive Softmax
在实际的计算中,指数的计算exp存在不稳定性,数值容易溢出,超过一定范围计算精度会下降等问题。
对于输入向量 s=[s1,s2,…,sN],Softmax 计算为:
\(p_i = \frac{e^{s_i}}{\sum_{j=1}^{N}{e^{s_j}}}\) 其中需要计算所有元素的指数和(分母)。

Safe Softmax

Online Softmax

std::vector<float> online_softmax(const std::vector<float>& src) {
std::vector<float> output(src.size());
float max_value = -99999999.f;
float sum = 0.0f;
float pre_value = 0.0f;
for (float val : src) {
max_value = std::max(max_value, val);
sum += sum * std::exp(pre_value - max_value) + std::exp(val - max_value);
pre_value = max_value;
}
// Calculate softmax values
for (size_t i = 0; i < src.size(); ++i) {
output[i] = std::exp(src[i] - max_value) / sum;
}
return output;
}
Online Softmax * Value
在上面的基础上补充: \(O_j \leftarrow O_{j-1} \frac{d_{j-1}e^{m_{j-1}-m_j}}{d_j} + \frac{e^{x_j-m_j}}{d_j} vj\)
动态更新全局最大值
假设将序列分成多个块,每个块可能包含不同的最大值。例如:
-
块1 的最大值为 m1=5,指数和为 \(l_1 = e^{s_1-5} + e^{s_2-5} + ...\)
-
块2 的最大值为m2=10,此时全局最大值更新为m=10,但块1的指数和\(l_1\) 是基于m1=5 计算的,需要重新调整。将之前块的指数和按新最大值重新缩放,确保全局一致性。
步骤1:初始化全局统计量
-
初始全局最大值 \(m_{global}=−{\infty}\)
-
初始全局指数和 Lglobal=0 \(L_{global}=0\)
步骤2:逐块处理
对于每个块 k:
-
计算当前块的局部最大值: \(m_{local}=max(s^{(k)})\)
-
更新全局最大值: \(m_{global}=max(m_{global},m_{local})\)
-
调整当前块的指数值: \(e^{s^{(k)}−m_{global}}\)
-
计算当前块的局部指数和: \(l_{local}=\sum_j{e^{s_j^{(k)}−m_{global}}}\)
-
调整之前所有块的指数和:
- 如果发现新的全局最大值 \(m_{global}\) 比之前的更大(即 mglobal>mprev),则需要将所有之前计算的指数和按比例缩放: \(L_{global}=L_{global}⋅ e^{m_{prev}−m_{global}}\) 这一步将之前基于旧最大值\(m_{global}\) 的指数和转换为新最大值 \(m_{global}\) 下的值。
-
累加当前块的指数和: \(L_{global}=L_{global}+l_{local}\)
步骤3:最终 Softmax 权重
- 对每个块中的元素 \(s_j^{(k)}\) ,其 Softmax 权重为: \(p_j^{(k)} = \frac{e^{s_j^{(k)} - m_{global}}}{L_{global}}\)
写入 HBM 的步骤
-
动态调整:在计算过程中,若发现新的全局最大值 \(m_i^{new}\) ,需对之前缓存的中间结果 \(O_i\) 进行缩放。
-
累加当前块:将当前块的注意力计算结果(调整后的 \(\tilde{P_{i,j}}V_j\) )累加到输出矩阵 \(O_i\)
-
归一化并写入:用最新的全局指数和 \(l_i^{new}\) 归一化结果,然后将 \(O_i\) 写回 HBM,释放 GPU 缓存。
显存节省的核心原因
- 传统方法:需存储 8000×8000=64000000个元素的中间矩阵。
- FlashAttention:
- 每次仅处理一个 100×100的块(占显存 10000个元素)。
- 最终输出矩阵O 占显存 8000×64=512000个元素。
- 显存占用从 O(N^2)降至 O(N)。
- 在GPU的高速缓存(SRAM)中逐块计算,避免一次性处理大矩阵。