##
Loss Function 损失函数
用于量化模型预测值与真实值之间差异的函数,其核心目标是通过最小化该差异来优化模型参数。
-
评估性能:衡量模型预测的准确性,值越小表示预测越接近真实值。
- 指导优化:通过梯度下降等算法调整模型参数,使损失最小化。
- 问题类型:回归选MSE/MAE,分类选交叉熵/Hinge损失。
通过合理选择损失函数,可显著提升模型性能。例如,图像分类常用交叉熵,房价预测多用MSE。
Cross Entropy是信息论中用于衡量两个概率分布差异的重要指标
在分类任务中:
- 真实分布 *P*:通常是标签的 one-hot 编码(如真实类别为3,则 P=[0,0,0,1,0,…])。
- 预测分布 *Q*:模型输出的概率分布(如 Softmax 后的结果)。
交叉熵损失函数的目标是让预测分布 Q 逼近真实分布 P。其数学形式为:
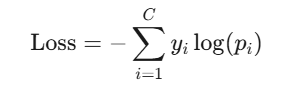
- C:类别总数。
- yi:真实标签的第 i 个分量(0 或 1)。
- pi:模型预测的第 i 个类别的概率。(需满足 ∑pi=1)
激活函数
Sigmoid
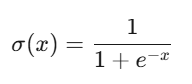
- 输出范围:(0, 1)
- 优点:输出可解释为概率,适用于二分类输出层。
- 缺点:梯度消失:当输入绝对值较大时,导数接近0,导致深层网络难以训练。
- 应用场景:二分类输出层
Tanh(双曲正切)
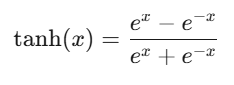
ReLU(Rectified Linear Unit)
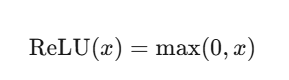
Leaky ReLU
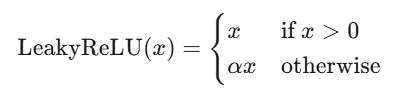
Softmax
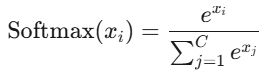
- 输出范围:(0,1),且和为1
- 特点:将输出转换为概率分布,用于多分类输出层(配合交叉熵损失)。
- 注意:输入值较大时可能数值溢出,需配合Log-Softmax或稳定化技巧。
激活函数选择指南
| 场景 | 推荐激活函数 | 理由 |
|---|---|---|
| 二分类输出层 | Sigmoid | 输出概率值,适配交叉熵损失。 |
| 多分类输出层 | Softmax | 输出归一化概率分布。 |
| 隐藏层(通用) | ReLU/Leaky ReLU/Swish | 计算高效,缓解梯度消失,适合深层网络。 |
| RNN/LSTM隐藏层 | Tanh | 零中心化,梯度幅度适中,避免输出漂移。 |
| 对抗死亡神经元问题 | Leaky ReLU/PReLU | 允许负区间梯度,保持神经元活性。 |
| 轻量级模型 | ReLU | 计算简单,节省资源。 |
优化器
用于调整模型参数以最小化损失函数的核心组件,其核心作用是通过梯度信息指导参数更新方向和步长。
SGD(随机梯度下降)
-
公式:
θ = θ - lr * ∇J(θ) -
特点:每次用单个样本或小批量样本计算梯度,更新参数。
-
优点:简单高效,适合大规模数据。
-
缺点:易陷入局部极小值,震荡明显。
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
Adam(Adaptive Moment Estimation)
为每个参数维护独立的自适应学习率:
# 使用Adam优化器(自动调整各参数的学习率)
optimizer = optim.Adam(model.parameters(), lr=0.001) # 初始lr仅作为参考基准
# 训练循环中,参数更新方式与SGD一致
optimizer.step()
内部机制:
- Adam 根据梯度的一阶矩(均值)和二阶矩(方差)动态调整每个参数的学习率。
- 实际更新公式:
param = param - lr * m_t / (sqrt(v_t) + eps)其中m_t和v_t是动量项。
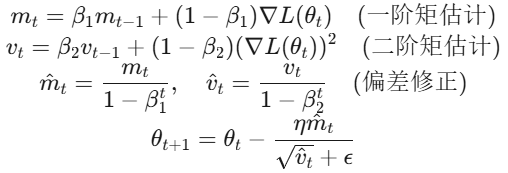
- 参数默认值:β1=0.9,β2=0.999,ϵ=1e−8
- 特点:
- 结合Momentum和RMSprop,自适应调整学习率。
- 适用于大多数深度学习任务,尤其是默认选择。
选择策略
| 优化器类型 | 适用场景 | 注意事项 |
|---|---|---|
| SGD/Momentum | 简单模型、需精细调参 | 需配合学习率调度器使用 |
| Adam/AdamW | 大多数深度学习任务(默认首选) | 注意权重衰减参数设置 |
| 自适应优化器 | 稀疏数据、特征分布差异大 | 避免用于RNN等动态网络结构 |
| 二阶优化器 | 小规模模型、需快速收敛 | 计算成本高,工业级应用较少 |
学习率
- 更新速度:高学习率(如0.1)可能导致训练不稳定甚至发散,低学习率(如0.001)会减缓收敛速度,易陷入局部最优。
- 稳定性:合理的学习率能帮助模型平稳收敛到全局最优或较好的局部最优