Transformer原理

Transformer结构

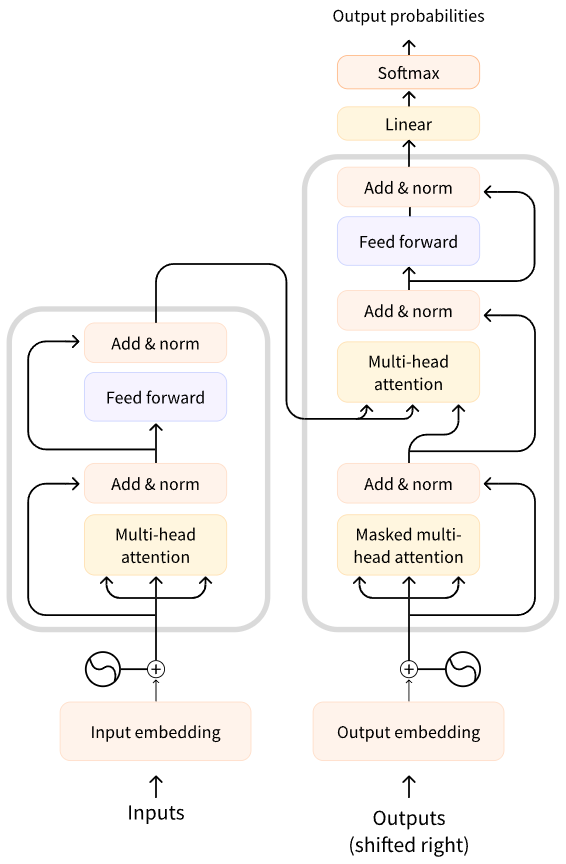
1. Input Embedding

对于输入文本序列，先通过Input Embedding 将每个单词转换为其相对应的向量表示。

在送入编码器端建模其上下文语义之前，在词嵌入中加入位置编码（Positional Encoding）。

Positional Encoding（位置编码） 来显式地为输入的词向量添加位置信息，使得模型能够利用这些信息来区分不同位置的词。

为什么 Transformer 需要 Positional Encoding？

Transformer 主要依赖 Self-Attention 机制，而 Self-Attention 计算时并不会保留输入序列的位置信息。换句话说，Self-Attention 关注的是词与词之间的关系，但不关心它们在序列中的先后顺序。

例如：

Positional Encoding 的实现

常见的 Positional Encoding 方法有：

1. 绝对位置编码（Sinusoidal Positional Encoding）

论文 Attention Is All You Need 采用了一种基于正弦和余弦函数的编码方式： \(PE_{(pos, 2i)} = \sin(pos / 10000^{2i/d})\)

\[PE_{(pos,2i+1)}=cos⁡(pos/10000^{2i/d})\]

其中：

pos 是单词在序列中的索引（位置）。
i 是 embedding 维度的索引（偶数位置用 sin，奇数位置用 cos）。
d 是 embedding 维度大小。

优点：

允许 Transformer 外推到比训练数据更长的序列（无需固定长度）。
通过不同频率的三角函数，使模型能够学习不同粒度的相对位置信息。

代码实践

class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len=80):
        super().__init__()
        self.d_model = d_model

        pe = torch.zeros(max_seq_len, d_model) # (L, D)
        for pos in range(max_seq_len):
            for i in range(0, d_model, 2):
                pe[pos, i] = math.sin(pos / (10000 ** (i / d_model)))
                pe[pos, i + 1] = math.cos(pos / (10000 ** (i / d_model)))

        pe = pe.unsqueeze(0) # 增加张量维度 改变shape (1, L, D)
		
        self.register_buffer('pe', pe)

为什么要 unsqueeze(0)？

在 Transformer 中，pe（Positional Encoding）最终需要 与输入的 token embedding 进行加法运算：

x = token_embedding + pe

而 token embedding 的形状通常是：

torch.Size([batch_size, seq_length, d_model])  # (B, L, D)

为了匹配 batch 维度（B），pe 需要变成 (1, L, D)，这样 PyTorch 会在计算时自动进行 广播（broadcasting），让 pe 适用于所有 batch。

2. Self-Attention

Self-Attention（自注意力机制）是一种计算序列中不同位置的元素之间关系的方法，它可以捕捉全局依赖关系，即在处理每个词时考虑整个输入序列，而不仅仅是局部上下文。

Self-Attention 计算流程

假设我们有一个长度为 nnn 的输入序列，每个 token 通过 embedding 得到向量表示，形状为： \(X \in \mathbb{R}^{n \times d}\) 其中：

n是序列长度（tokens 数量）。
d 是 embedding 维度。

Self-Attention 主要由 三组 learnable 矩阵 进行计算：

Query 矩阵（Q）：查询向量，表示当前 token 在注意力计算中的 “询问” 角色。
Key 矩阵（K）：键向量，表示当前 token 的 “身份信息”。
Value 矩阵（V）：值向量，表示当前 token 携带的信息内容。

这三组矩阵通过线性变换得到：

\[Q = X W_Q, \quad K = X W_K, \quad V = X W_V\]

其中 \(W_Q, W_K, W_V \in \mathbb{R}^{d \times d_k}\) 是可训练参数。

Step 1: 计算注意力分数（Score）

用 Query 和 Key 计算相似度（点积）： \(\text{Score} = Q K^T\) 结果是一个 n x n 的矩阵，表示每个 token 与其他 token 之间的相关性。

Step 2: 归一化（Softmax）

对每一行的注意力分数进行 Softmax 归一化，得到注意力权重： \(\text{Attention} = \text{Softmax}(\frac{Q K^T}{\sqrt{d_k}})\) 这里 \(\sqrt{d_k}\) 是缩放因子，防止点积值过大影响梯度。d_k表示经过线性变换后得到的 Query 和 Key 向量的维度。

原始输入的 embedding 通常维度为 d，通过乘以 W_Q、W_K 或 W_V 后，得到的向量维度变为 d_k（有时 Value 的维度记作 d_v），这相当于对输入进行了降维或重新映射，方便后续的注意力计算。

在多头注意力（Multi-Head Attention）中，如果模型总的 embedding 维度为 d，通常会将其分割为 h 个头，每个头的维度就常常设置为 d_k = d/h。这样每个头可以独立捕捉输入序列中的不同关系模式，然后再将各个头的结果拼接起来，形成整体的输出。

Step 3: 计算加权和

最终用注意力权重对 Value 进行加权求和： \(\text{Output} = \text{Attention} \times V\) 这样，每个 token 的表示都综合了整个序列的上下文信息。

代码实践

class MultiHeadAttention(nn.Module):
    def __init__(self, heads, d_model, dropout=0.1):
        super().__init__()

        self.d_model = d_model
        self.d_k = d_model // heads  # d_k 代表 每个注意力头的维度
        self.h = heads

        self.q_linear = nn.Linear(d_model, d_model)
        self.v_linear = nn.Linear(d_model, d_model)
        self.k_linear = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)  # Dropout 层，用于在训练过程中随机丢弃一部分神经元，10% 的神经元会被随机屏蔽，防止模型对特定路径过拟合
        self.out = nn.Linear(d_model, d_model)

    '''
 缩放点积注意力（Scaled Dot-Product Attention），用于计算 Q, K, V 之间的注意力权重，并返回加权的 V 作为输出
 q（Query）：查询矩阵，形状 (batch_size, heads, seq_len_q, d_k)
 k（Key）：键矩阵，形状 (batch_size, heads, seq_len_k, d_k)
 v（Value）：值矩阵，形状 (batch_size, heads, seq_len_k, d_v)
 在 Self-Attention 里，通常 seq_len_q == seq_len_k，因为 Query 和 Key 来自 同一序列
''' 
	def attention(q, k, v, d_k, mask=None, dropout=None):
        # 计算 Query 与 Key 之间的相似度
        # 除以 sqrt(d_k) 进行 缩放（scaled），防止 d_k 过大导致 softmax 输出过于集中（梯度消失问题）
        # k 转置后形状：(batch_size, heads, d_k, seq_len_k)
        # scores形状：(batch_size, heads, seq_len_q, seq_len_k)
        scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)

        if mask is not None:
            # 扩展维度，使 mask 适配注意力 scores 形状
            mask = mask.unsqueeze(1) 
            # mask == 0 的位置被填充为 -1e9，使得 softmax 计算时这些位置的概率趋近于 0，防止注意力分配到这些无效位置。

            scores = scores.masked_fill(mask == 0, -1e9) 

        # 在最后一个维度（seq_len_k 维度）上计算 softmax，确保 每个 Query 位置的注意力分数归一化为概率分布
        scores = F.softmax(scores, dim=-1)  

        if dropout is not None:
            scores = dropout(scores)  # 训练时启用，测试时关闭

        # 将 scores 作为 注意力权重，对 V 进行加权求和。 V 代表实际的信息，scores 决定了 关注哪些 V 的信息
        output = torch.matmul(scores, v)  
        # 输出形状：(batch_size, heads, seq_len_q, d_v)

        return output

Mask作用

mask == 0 的位置被填充为 -1e9，使得 softmax 计算时这些位置的概率趋近于 0，防止注意力分配到这些无效位置。

应用场景：

Padding Mask：防止对填充 (PAD) 位置计算注意力。
Look-Ahead Mask（未来信息屏蔽）：在解码器中，防止当前 token 看到未来 token。

Softmax

Softmax 是一种激活函数，常用于多分类问题中的输出层。它可以将一个包含任意实数的向量转换为概率分布，使得所有输出值的总和为 1，从而适合作为分类任务的最终决策依据。

对于一个具有 nnn 个类别的分类问题，假设输入是一个未归一化的得分向量 z=[z1,z2,…,zn]，则 Softmax 函数的计算公式为： \(\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}\) Softmax 的作用

将数值转化为概率 由于 Softmax 的输出是一个概率分布（总和为 1），可以用于多分类问题的决策。
增强数值的可区分性 大的数值会变得更大，较小的数值会被抑制，从而提高模型对高置信度类别的偏向性。
用于交叉熵损失函数 在多分类问题中，Softmax 结合 交叉熵损失函数（Cross-Entropy Loss），可以有效训练分类模型。

Softmax 与 Sigmoid 的区别

对比项	Softmax	Sigmoid
适用场景	多分类（多个类别）	二分类（单个类别）
输出范围	(0,1) 且总和为 1	(0,1) 但不归一化
决策方式	选择概率最大类别	选择概率是否大于 0.5

3. 前馈层（Feed-Forward Layer, FFN）

前馈层（Feed-Forward Layer, FFN） 是 Transformer 结构中的 非自注意力 计算部分，主要作用是对每个 token 进行独立的特征变换和非线性映射。它可以看作是一个逐 token 的 MLP（多层感知机），用于增强模型的表达能力。

结构

一个标准的 Transformer 前馈层（FFN） 由 两个全连接层（线性变换）和一个 激活函数 组成： \(\text{FFN}(x) = \max(0, x W_1 + b_1) W_2 + b_2\)

代码实现

import torch
import torch.nn as nn

class FeedForward(nn.Module):
    def __init__(self, d_model, d_ff=2048, dropout=0.1):
        super().__init__()
        self.fc1 = nn.Linear(d_model, d_ff)  # 第一层：d_model -> d_ff
        self.fc2 = nn.Linear(d_ff, d_model)  # 第二层：d_ff -> d_model
        self.relu = nn.ReLU()  # 激活函数 f(x)=max(0,x) 简单高效，避免梯度消失, 比 sigmoid/tanh 更适合深度学习
        self.dropout = nn.Dropout(dropout)  # 防止过拟合

    def forward(self, x):
        return self.fc2(self.dropout(self.relu(self.fc1(x))))

为什么需要前馈层FFN？

1. 提高表达能力

Self-Attention 主要关注不同 token 之间的信息交互，但对于单个 token 的特征提取能力较弱。
前馈层类似 CNN/MLP，提供非线性变换，提升模型的表示能力。

2. 维度扩展

Transformer 论文中 d_ff = 4 \* d_model，让 FFN 有更大的学习容量。
第一层扩展特征维度，第二层再压缩回去，类似于 瓶颈结构（Bottleneck）。

3. 逐 token 计算

FFN 对每个 token 独立计算，不考虑序列关系，可以并行计算，加快训练速度。

FFN 在 Transformer 中的位置

在 Transformer Encoder / Decoder 的每一层，结构如下：

输入序列 -> Self-Attention -> Add & Norm -> 前馈层（FFN） -> Add & Norm -> 输出

层归一化（Layer Normalization, LayerNorm）

层归一化 是用于稳定训练的一种方法，它归一化每个样本的特征维度，以减少不同批次间的分布变化。

对于输入 x： \(\hat{x}_i = \frac{x_i - \mu}{\sigma} * \gamma + \beta\)

其中：

μ 和 σ 是在 同一层 的所有特征维度上的均值和标准差
γ 和 β 是可学习的缩放和平移参数
归一化后，每一层的输入分布更稳定，使模型更易训练

为什么使用 LayerNorm？

Transformer 处理序列数据，BatchNorm 依赖批次统计信息，而 LayerNorm 只依赖自身层，不受批次大小影响
适用于变长序列（Transformer 需要处理不定长输入）
适用于自回归模型（Transformer 需要 token-by-token 生成）

代码实践

class Norm(nn.Module):

    def __init__(self, d_model, eps=1e-6):
        super().__init__()
        self.size = d_model

        # 层归一化
        self.alpha = nn.Parameter(torch.ones(self.size))
        self.bias = nn.Parameter(torch.zeros(self.size))

        self.eps = eps

    def forward(self, x):
        norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
        return norm

在torch中专门的LayerNorm：

x = torch.randn(2, 5, 10)  # batch_size=2, seq_len=5, embedding_dim=10
layer_norm = nn.LayerNorm(10)  # 归一化维度为 10
output = layer_norm(x)
print(output.shape)  # (2, 5, 10)

残差连接

残差连接（Residual Connection）是一种缓解梯度消失问题的方法，最早由 ResNet（深度残差网络） 提出，并被 Transformer 广泛使用。

给定输入 x 和变换函数 F(x)： \(\text{Output} = x + F(x)\) 其中：

x是原始输入（跳跃连接）
F(x)是经过 线性变换 + 激活函数 处理的输入
最后进行 层归一化（LayerNorm）

Transformer 里的残差连接 + 层归一化

Transformer 每个子层（自注意力 & 前馈网络）都使用： \(\text{LayerNorm}(\text{Input} + \text{SubLayer}(Input))\)

代码实践

import torch.nn as nn

class ResidualConnection(nn.Module):
    def __init__(self, d_model, dropout=0.1):
        super(ResidualConnection, self).__init__()
        self.norm = nn.LayerNorm(d_model)  # 层归一化
        self.dropout = nn.Dropout(dropout)  # 防止过拟合

    def forward(self, x, sublayer):
        return self.norm(x + self.dropout(sublayer(x)))  # 残差连接 + 归一化

Encoder

class EncoderLayer(nn.Module):
    def __init__(self, d_model, heads, dropout=0.1):
        super().__init__()
        self.norm_1 = Norm(d_model)
        self.norm_2 = Norm(d_model)
        self.attn = MultiHeadAttention(heads, d_model, dropout=dropout)
        self.ff = FeedForward(d_model, dropout=dropout)
        self.dropout_1 = nn.Dropout(dropout)
        self.dropout_2 = nn.Dropout(dropout)

    def forward(self, x, mask):
        attn_output = self.attn(x, x, x, mask)
        attn_output = self.dropout_1(attn_output)
        x = x + attn_output
        x = self.norm_1(x)

        # Feed-forward
        ff_output = self.ff(x)
        ff_output = self.dropout_2(ff_output)
        x = x + ff_output
        x = self.norm_2(x)
        return x


def get_clones(module, N):
    return nn.ModuleList([module for _ in range(N)])


class Encoder(nn.Module):

    # 词汇表大小, 嵌入维度, 编码器层数, 多头注意力中的头数
    def __init__(self, vocab_size, d_model, N, heads, dropout):
        super().__init__()
        self.N = N
        self.embed = Embedder(vocab_size, d_model)
        self.pe = PositionalEncoder(d_model)
        self.layers = get_clones(EncoderLayer(d_model, heads, dropout), N)
        self.norm = Norm(d_model)

    def forward(self, src, mask):
        x = self.embed(src)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, mask)
        return self.norm(x)

Decoder

class DecoderLayer(nn.Module):
    # d_model: 词嵌入维度, heads: 多头注意力中的头数, dropout: dropout 概率
    def __init__(self, d_model, heads, dropout=0.1):
        super().__init__()
        self.norm_1 = Norm(d_model)
        self.norm_2 = Norm(d_model)
        self.norm_3 = Norm(d_model)

        self.dropout_1 = nn.Dropout(dropout)
        self.dropout_2 = nn.Dropout(dropout)
        self.dropout_3 = nn.Dropout(dropout)

        self.attn_1 = MultiHeadAttention(heads, d_model, dropout=dropout)
        self.attn_2 = MultiHeadAttention(heads, d_model, dropout=dropout)
        self.ff = FeedForward(d_model, dropout=dropout)

    def forward(self, x, e_outputs, src_mask, trg_mask):
        # 自注意力 (attn_1)：首先，计算目标序列的自注意力，用 trg_mask 来屏蔽掉不必要的部分
        attn_output_1 = self.attn_1(x, x, x, trg_mask)
        x = self.norm_1(x + self.dropout_1(attn_output_1))

        # 交叉注意力 (attn_2)：然后，计算目标序列与源序列之间的注意力，用 src_mask 来屏蔽掉源序列中的无效部分
        attn_output_2 = self.attn_2(x, e_outputs, e_outputs, src_mask)
        x = self.norm_2(x + self.dropout_2(attn_output_2))

        # 通过前馈神经网络处理输出
        ff_output = self.ff(x)
        # 每个操作后都有残差连接和层归一化
        x = self.norm_3(x + self.dropout_3(ff_output))

        return x


class Decoder(nn.Module):
    # vocab_size: 词汇表大小, d_model: 词嵌入维度, N: 解码器层数, heads: 多头注意力中的头数, dropout: dropout 概率
    def __init__(self, vocab_size, d_model, N, heads, dropout):
        super().__init__()
        self.N = N
        self.embed = Embedder(vocab_size, d_model)
        self.pe = PositionalEncoder(d_model, dropout=dropout)
        self.layers = get_clones(DecoderLayer(d_model, heads, dropout), N)
        self.norm = Norm(d_model)

    def forward(self, trg, e_outputs, src_mask, trg_mask):
        x = self.embed(trg)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, e_outputs, src_mask, trg_mask)
        return self.norm(x)

EncoderLayer 和 DecoderLayer的区别

应用场景

EncoderLayer：
- 用于理解输入序列，如文本分类、语义理解。
- 在BERT等模型中，仅使用编码器堆叠。
DecoderLayer：
- 用于生成序列，如机器翻译、文本生成。
- 在GPT等模型中，仅使用解码器堆叠（但设计可能不同，例如GPT使用无交叉注意力的解码器）。

结构差异

EncoderLayer 结构：

复制

输入 → 自注意力 → 残差连接 + 层归一化 → 前馈网络 → 残差连接 + 层归一化

DecoderLayer 结构：

复制

输入 → 掩码自注意力 → 残差连接 + 层归一化 → 交叉注意力（与编码器输出交互） → 残差连接 + 层归一化 → 前馈网络 → 残差连接 + 层归一化

解码器层比编码器层多了一个交叉注意力模块。

注意力机制的不同

EncoderLayer
- 仅包含自注意力（Self-Attention）：编码器层通过自注意力机制处理输入序列，关注序列内部各位置之间的关系（例如句子中词语之间的依赖关系）。
- 无掩码（No Masking）：自注意力可以访问整个输入序列的所有位置，没有未来信息的遮蔽。
DecoderLayer
- 包含两种注意力：
  1. 掩码自注意力（Masked Self-Attention）：在生成当前输出时，只能看到当前位置及之前的信息（通过掩码遮蔽未来位置）。
  2. 交叉注意力（Cross-Attention）：解码器的注意力会额外关注编码器的输出，用于将输入序列的信息整合到输出生成中（例如翻译时参考源语言的信息）。

处理数据的方式

EncoderLayer
- 目标是压缩输入序列的全局信息，将其转化为高层语义表示（如句子级别的特征）。
- 每个位置的信息会被编码成一个上下文相关的向量。
DecoderLayer
- 目标是逐步生成输出序列（如逐词生成翻译结果）。
- 在生成每个位置时，需要结合两个信息：
  1. 已生成部分的掩码自注意力结果（历史信息）。
  2. 编码器输出的全局信息（通过交叉注意力）。

掩码的作用

编码器层不需要掩码，因为输入是完整的已知序列。
解码器层在训练时通过掩码自注意力确保生成过程是自回归的（即只能看到过去的信息）。

总结对比表

特性	EncoderLayer	DecoderLayer
注意力类型	自注意力	掩码自注意力 + 交叉注意力
掩码使用	无	掩码自注意力遮蔽未来信息
输入依赖	仅自身输入序列	自身输入 + 编码器输出
目标	提取全局特征	自回归生成输出序列
典型应用	BERT、ViT	GPT、机器翻译