Introduction
文章提出了一种有效的几何范围查询方案(EGRQ)来支持加密空间数据的搜索和访问控制。在EGRQ中使用了安全的KNN计算、多项式拟合技术和保顺的加密来保护范围查询的安全性和私密性,为了提高效率利用R-tree来减少搜索空间和匹配时间。
System Model
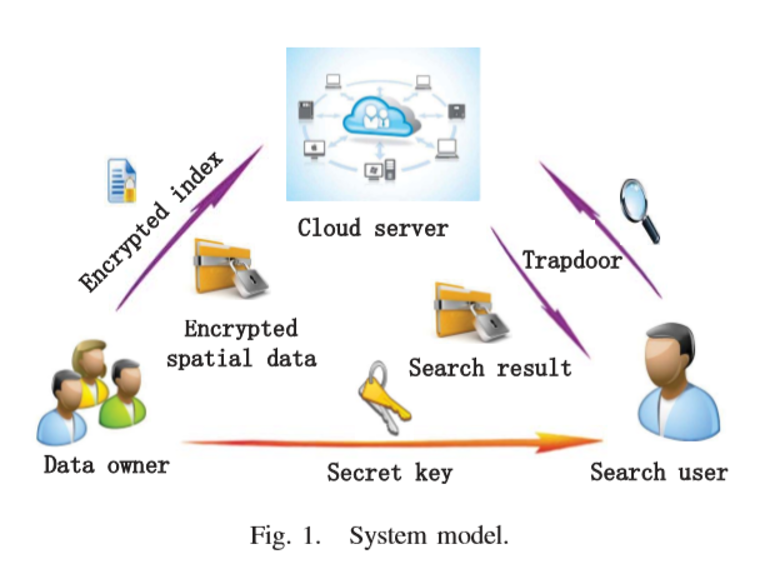
-
数据拥有者
数据所有者的主要任务是将其空间数据以密文(utilizing AES)的形式提交给云服务器。为了提高检索效率,对于每个原始数据,数据所有者将创建一个与之相关联的加密索引。然后密文和索引都被发送到云服务器。
-
云服务提供商
云服务器收到查询请求,通过一系列计算将相应的搜索结果返回。
-
查询用户
当密钥传递给查询用户时,查询用户发送相应的加密查询请求trapdoor,在接收到来自云服务器的搜索结果后,使用密钥离线解密这些结果。
Preliminaries
Security KNN Computation
安全KNN计算通常由四部分组成:SKC_Initialization、SkC_GenIndex、SkC_GenTrapdoor和SkC_Query。
Order-Preserving Encryption
OPE指加密后可以保持数据顺序不变,如果m1 > m2,[m1] > [m2],其中我们用[·]表示密文。由于这种特殊的特性,许多安全范围查询场景,如位置查找、数据挖掘和其他基于位置的服务都采用了OPE。
文章中利用OPE的特性来实现加密空间数据之间的比较操作,从而缩小查询范围,显著提高搜索效率。
Polynomial Fitting Technique
在文章中多项式拟合被应用到范围查询模型中来生成trapdoor的一部分。具体来说,如图2所示,搜索范围可以分成两个曲线(θ1 ,θ2),取两条曲线上距离相等的10个点。将生成两条拟合曲线并命名θ1*和θ2*,式子如下。
\(θ^{*}_{1}(x) = a_0 +a_1x +a_2x^2 +···+a_nx^N \\
θ^{*}_{2}(x) =b_0 +b_1x +b_2x^2 +···+b_nx^N\)
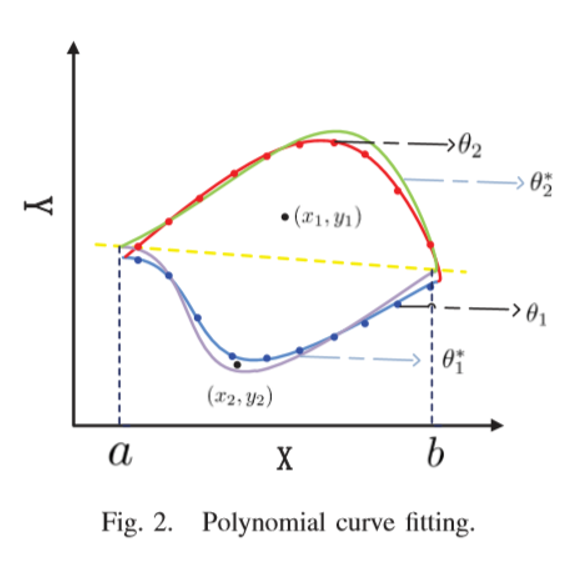
如图2所示,假设X的定义域是[a,b],可以判断出(x1, y1)是在给定范围内。
多项式曲线拟合可以用来拟合任何给定的曲线,并检查点是否在该曲线内。然而,由于曲线拟合是一种近似算法,利用拟合曲线代替实际曲线,不可避免地会产生误差。
Access Control Strategy
文章设计了一种新的空间数据访问控制策略,使得每个搜索用户只能访问自己授权的用户数据。例如如果将角色ai分配给搜索用户j,那么只能将与ai相关的原始空间数据查询给搜索用户j。
R-Tree
R-Tree的核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形,这个最小外接矩形就成为上一层的一个节点。
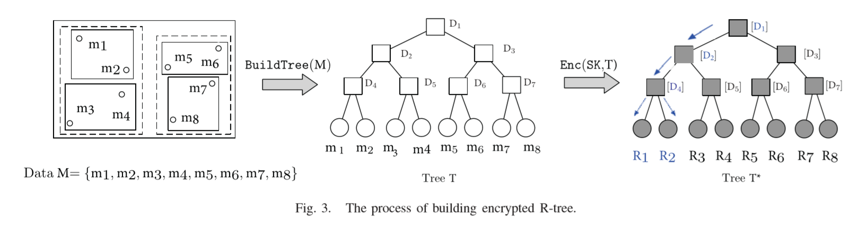
- R-Tree从根节点开始,遍历整个树,找到与给定搜索矩形相交的所有最深的非叶节点(如果存在的话),否者返回空。
- 对于上面非叶节点中包含的每个点,检查它是否满足节中说明的条件。如果满足,将这些点返回给搜索用户。否者返回空。
PROPOSED SCHEME
-
Initialization
-
GenIndex
-
GenTrapdoor
-
Query
原文:Enabling Efficient and Geometric Range Query With Access Control Over Encrypted Spatial Data